 login/create account
login/create account
Monochromatic reachability in arc-colored digraphs
Conjecture For every  , there exists an integer
, there exists an integer 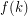 such that if
such that if  is a digraph whose arcs are colored with
is a digraph whose arcs are colored with  colors, then
colors, then  has a
has a  set which is the union of
set which is the union of 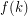 stables sets so that every vertex has a monochromatic path to some vertex in
stables sets so that every vertex has a monochromatic path to some vertex in  .
.
 , there exists an integer
, there exists an integer 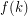 such that if
such that if  is a digraph whose arcs are colored with
is a digraph whose arcs are colored with  colors, then
colors, then  has a
has a  set which is the union of
set which is the union of 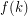 stables sets so that every vertex has a monochromatic path to some vertex in
stables sets so that every vertex has a monochromatic path to some vertex in  .
. In the particular case of tournaments (and more generally when the stabilty number of  is bounded), it has been proved by Bousquet, Lochet, and Thomassé [BLT].
is bounded), it has been proved by Bousquet, Lochet, and Thomassé [BLT].
Bibliography
[BLT] Nicolas Bousquet, William Lochet, Stéphan Thomassé: A proof of the Erdős-Sands-Sauer-Woodrow conjecture,
[SSW] B. Sands, N. Sauer and R. Woodrow, On monochromatic paths in edge-coloured digraphs. Journal of Combinatorial Theory, Series B, 33, (1982), 271--275.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University