 login/create account
login/create account
Monochromatic reachability in edge-colored tournaments (Solved)
Problem For every  , is there a (least) positive integer
, is there a (least) positive integer 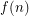 so that whenever a tournament has its edges colored with
so that whenever a tournament has its edges colored with  colors, there exists a set
colors, there exists a set  of at most
of at most 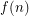 vertices so that every vertex has a monochromatic path to some point in
vertices so that every vertex has a monochromatic path to some point in  ?
?
 , is there a (least) positive integer
, is there a (least) positive integer 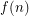 so that whenever a tournament has its edges colored with
so that whenever a tournament has its edges colored with  colors, there exists a set
colors, there exists a set  of at most
of at most 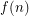 vertices so that every vertex has a monochromatic path to some point in
vertices so that every vertex has a monochromatic path to some point in  ?
? This problem first appears in print in a lovely paper of Sands, Sauer, and Woodrow [SSW], where they prove that 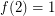 . Actually, they prove a much stronger theorem. They show that for every 2-edge-colored digraph
. Actually, they prove a much stronger theorem. They show that for every 2-edge-colored digraph  (even infinite) there exists an independent set
(even infinite) there exists an independent set 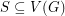 so that every vertex has a monochromatic path to some point in
so that every vertex has a monochromatic path to some point in  .
.
It is open whether 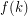 is finite for every
is finite for every 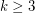 . The smallest open case,
. The smallest open case, 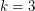 , is already quite interesting; In [SSW] the authors ask if
, is already quite interesting; In [SSW] the authors ask if 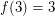 .
.
Bibliography
*[SSW] B. Sands, N. Sauer, R. Woodrow, On monochromatic paths in edge-coloured digraphs. J. Combin. Theory Ser. B 33 (1982), no. 3, 271--275. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University