 login/create account
login/create account
tournament
PTAS for feedback arc set in tournaments ★★
Question Is there a polynomial time approximation scheme for the feedback arc set problem for the class of tournaments?
Keywords: feedback arc set; PTAS; tournament
Monochromatic reachability or rainbow triangles ★★★
Author(s): Sands; Sauer; Woodrow
In an edge-colored digraph, we say that a subgraph is rainbow if all its edges have distinct colors, and monochromatic if all its edges have the same color.
Problem Let  be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path?
 be a tournament with edges colored from a set of three colors. Is it true that
be a tournament with edges colored from a set of three colors. Is it true that  must have either a rainbow directed cycle of length three or a vertex
must have either a rainbow directed cycle of length three or a vertex  so that every other vertex can be reached from
so that every other vertex can be reached from  by a monochromatic (directed) path?
by a monochromatic (directed) path? Keywords: digraph; edge-coloring; tournament
Monochromatic reachability in edge-colored tournaments ★★★
Author(s): Erdos
Problem For every  , is there a (least) positive integer
, is there a (least) positive integer 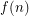 so that whenever a tournament has its edges colored with
so that whenever a tournament has its edges colored with  colors, there exists a set
colors, there exists a set  of at most
of at most 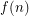 vertices so that every vertex has a monochromatic path to some point in
vertices so that every vertex has a monochromatic path to some point in  ?
?
 , is there a (least) positive integer
, is there a (least) positive integer 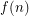 so that whenever a tournament has its edges colored with
so that whenever a tournament has its edges colored with  colors, there exists a set
colors, there exists a set  of at most
of at most 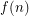 vertices so that every vertex has a monochromatic path to some point in
vertices so that every vertex has a monochromatic path to some point in  ?
? Keywords: digraph; edge-coloring; tournament

 Drupal
Drupal CSI of Charles University
CSI of Charles University