 login/create account
login/create account
Galois connections
A diagram about funcoids and reloids ★★
Author(s): Porton
Define for posets with order  :
:
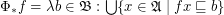 ;
;
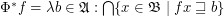 .
.
Note that the above is a generalization of monotone Galois connections (with 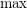 and
and  replaced with suprema and infima).
replaced with suprema and infima).
Then we have the following diagram:

What is at the node "other" in the diagram is unknown.
Conjecture "Other" is 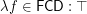 .
.
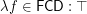 .
. Question What repeated applying of 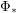 and
and 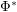 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 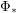 and/or
and/or 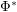 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets?
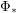 and
and 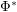 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 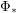 and/or
and/or 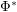 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets? Keywords: Galois connections

 Drupal
Drupal CSI of Charles University
CSI of Charles University