 login/create account
login/create account
A diagram about funcoids and reloids
Define for posets with order  :
:
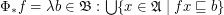 ;
;
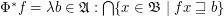 .
.
Note that the above is a generalization of monotone Galois connections (with  and
and  replaced with suprema and infima).
replaced with suprema and infima).
Then we have the following diagram:
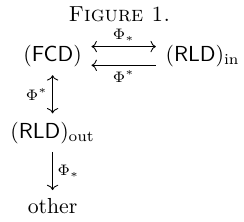
What is at the node "other" in the diagram is unknown.
Conjecture "Other" is 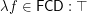 .
.
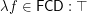 .
. Question What repeated applying of 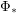 and
and 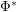 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 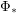 and/or
and/or 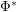 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets?
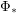 and
and 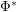 to "other" leads to? Particularly, does repeated applying
to "other" leads to? Particularly, does repeated applying 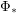 and/or
and/or 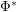 to the node "other" lead to finite or infinite sets?
to the node "other" lead to finite or infinite sets? See Algebraic General Topology for definitions of used concepts.
The known part of the diagram is considered in this file.
Bibliography
* indicates original appearance(s) of problem.
The diagram was with an error
On November 26th, 2016 porton says:
My diagram was with an error. I have uploaded a corrected version of the diagram.
--
Victor Porton - http://www.mathematics21.org

 Drupal
Drupal CSI of Charles University
CSI of Charles University
The value of node "other"
It seems that the node "other" is not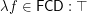 .
.
I conjecture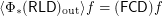 where
where  is the reloid defined by the cofinite filter on
is the reloid defined by the cofinite filter on 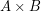 and thus
and thus 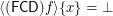 for all singletons
for all singletons 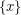 and
and 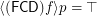 for every nontrivial atomic filter
for every nontrivial atomic filter  .
.
This is my very recent thoughts and yet needs to be checked.
-- Victor Porton - http://www.mathematics21.org