 login/create account
login/create account
Kalai, Gil
The Double Cap Conjecture ★★
Author(s): Kalai
Conjecture The largest measure of a Lebesgue measurable subset of the unit sphere of 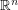 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 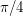 around the north and south poles.
around the north and south poles.
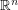 containing no pair of orthogonal vectors is attained by two open caps of geodesic radius
containing no pair of orthogonal vectors is attained by two open caps of geodesic radius 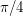 around the north and south poles.
around the north and south poles. Keywords: combinatorial geometry; independent set; orthogonality; projective plane; sphere
Cube-Simplex conjecture ★★★
Author(s): Kalai
Conjecture For every positive integer  , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 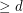 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube.
 , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 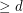 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University