 login/create account
login/create account
cube
Edge-antipodal colorings of cubes ★★
Author(s): Norine
We let 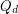 denote the
denote the  -dimensional cube graph. A map
-dimensional cube graph. A map 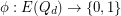 is called edge-antipodal if
is called edge-antipodal if 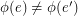 whenever
whenever 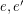 are antipodal edges.
are antipodal edges.
Conjecture If 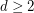 and
and 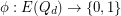 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 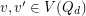 which are joined by a monochromatic path.
which are joined by a monochromatic path.
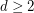 and
and 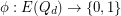 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 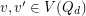 which are joined by a monochromatic path.
which are joined by a monochromatic path. Keywords: antipodal; cube; edge-coloring
Simplexity of the n-cube ★★★
Author(s):
Question What is the minimum cardinality of a decomposition of the  -cube into
-cube into  -simplices?
-simplices?
 -cube into
-cube into  -simplices?
-simplices? Keywords: cube; decomposition; simplex
Cube-Simplex conjecture ★★★
Author(s): Kalai
Conjecture For every positive integer  , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 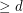 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube.
 , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 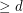 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University