 login/create account
login/create account
Edge-antipodal colorings of cubes
We let 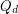 denote the
denote the  -dimensional cube graph. A map
-dimensional cube graph. A map 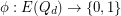 is called edge-antipodal if
is called edge-antipodal if 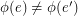 whenever
whenever 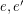 are antipodal edges.
are antipodal edges.
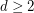 and
and 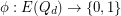 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 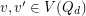 which are joined by a monochromatic path.
which are joined by a monochromatic path. This conjecture has been verified by hand for 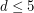 .
.
Bibliography
* indicates original appearance(s) of problem.
proof?
Let's suppose G is minimal counterexample. We are denote vertices as "x1 x2 x3 ..." xi={0|1} so, for example, "110...01" and "001...10" are antipodes. Consider G' is subgraph induced by x1=1. G' is lesser hypercube, so where exists connected pair of G'-antipodes, for clarification, "100001111" and "111110000". but ("100001111","000001111") and ("111110000","011110000" ) are edge-antipodes in G, so either ("100001111", "011110000") or ("000001111", "111110000") are connected! (And path length is equal to G dimension.)
Looks too simple, am I misunderstood something? Or where is my medal? :))
not quite!
the edge-coloring of the subcube consisting of those vertices with x1=1 need not be edge-antipodal.
Yes, indeed
Got it. edge-antipodes in G' are not antipodes in G, so can have same color. Thanks.
special case proven
We prove the conjecture in the special case where there is no square xyzt in the cube such that xy and zt get value 0, while yz and xt get value 1. The paper by Tomas Feder and Carlos Subi (submitted) can be found at
http://theory.stanford.edu/~tomas/antipod.ps

 Drupal
Drupal CSI of Charles University
CSI of Charles University
2-colorings of edges of the cube
Q_n denotes the n-dimensional cube. For any x in Q_n, x_bar denotes the antipodal of x in Q_n.
We conjecture the following: Conj1 Let c:E_n --> {0, 1} be a coloring of the edges of Q_n. Then, there exists a pair of antipodal points x, x_bar and a path p from x to x_bar that it is either monochromatic or it changes colors exactly once.
It is easy to see that this conjecture implies an affirmative answer to the "antipodal" coloring open problem. We have verified that Conj1 holds for dimensions n=2, 3, and 4. We have also found that if the coloring is simple, that is, it does not contain squares colored 0101, then Conj1 holds (in fact, we find a monochromatic path joining a pair of antipodals).