 login/create account
login/create account
antipodal
Edge-antipodal colorings of cubes ★★
Author(s): Norine
We let 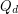 denote the
denote the 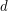 -dimensional cube graph. A map
-dimensional cube graph. A map 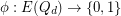 is called edge-antipodal if
is called edge-antipodal if 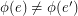 whenever
whenever 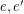 are antipodal edges.
are antipodal edges.
Conjecture If 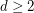 and
and 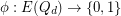 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 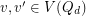 which are joined by a monochromatic path.
which are joined by a monochromatic path.
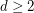 and
and 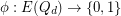 is edge-antipodal, then there exist a pair of antipodal vertices
is edge-antipodal, then there exist a pair of antipodal vertices 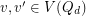 which are joined by a monochromatic path.
which are joined by a monochromatic path. Keywords: antipodal; cube; edge-coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University