 login/create account
login/create account
facet
Cube-Simplex conjecture ★★★
Author(s): Kalai
Conjecture For every positive integer  , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 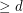 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube.
 , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 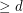 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube. 
 Drupal
Drupal CSI of Charles University
CSI of Charles University