 login/create account
login/create account
polytope
Durer's Conjecture ★★★
Conjecture Every convex polytope has a non-overlapping edge unfolding.
Cube-Simplex conjecture ★★★
Author(s): Kalai
Conjecture For every positive integer  , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 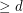 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube.
 , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 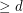 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube. Continous analogue of Hirsch conjecture ★★
Author(s): Deza; Terlaky; Zinchenko
Conjecture The order of the largest total curvature of the primal central path over all polytopes defined by  inequalities in dimension
inequalities in dimension  is
is  .
.
 inequalities in dimension
inequalities in dimension  is
is  .
. Average diameter of a bounded cell of a simple arrangement ★★
Author(s): Deza; Terlaky; Zinchenko
Conjecture The average diameter of a bounded cell of a simple arrangement defined by  hyperplanes in dimension
hyperplanes in dimension  is not greater than
is not greater than  .
.
 hyperplanes in dimension
hyperplanes in dimension  is not greater than
is not greater than  .
. Keywords: arrangement; diameter; polytope
Fat 4-polytopes ★★★
Author(s): Eppstein; Kuperberg; Ziegler
The fatness of a 4-polytope  is defined to be
is defined to be 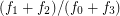 where
where 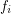 is the number of faces of
is the number of faces of  of dimension
of dimension  .
.
Question Does there exist a fixed constant  so that every convex 4-polytope has fatness at most
so that every convex 4-polytope has fatness at most  ?
?
 so that every convex 4-polytope has fatness at most
so that every convex 4-polytope has fatness at most  ?
? 
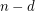 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University