 login/create account
login/create account
Eppstein, David
Fat 4-polytopes ★★★
Author(s): Eppstein; Kuperberg; Ziegler
The fatness of a 4-polytope  is defined to be
is defined to be 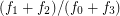 where
where 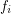 is the number of faces of
is the number of faces of  of dimension
of dimension  .
.
Question Does there exist a fixed constant  so that every convex 4-polytope has fatness at most
so that every convex 4-polytope has fatness at most  ?
?
 so that every convex 4-polytope has fatness at most
so that every convex 4-polytope has fatness at most  ?
? 
 Drupal
Drupal CSI of Charles University
CSI of Charles University