 login/create account
login/create account
Hirsch Conjecture (Solved)
(Originally appeared in [D], this discussion appears as [M].)
Many special cases of this conjecture have been verified, and in particular, the case of 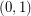 -polytopes was settled by Naddef by an elegant proof in [N], and further generalized in [MT]. However, in the general case, the Hirsch conjecture is known only for
-polytopes was settled by Naddef by an elegant proof in [N], and further generalized in [MT]. However, in the general case, the Hirsch conjecture is known only for 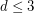 . It is even open if there is a polynomial upper bound on the diameter. Kalai and Kleitman [KK] found a quasi-polynomial bound by proving that the diameter is bounded by
. It is even open if there is a polynomial upper bound on the diameter. Kalai and Kleitman [KK] found a quasi-polynomial bound by proving that the diameter is bounded by 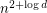 .
.
The special case of Hirsch Conjecture, the  -step conjecture, asserts that the diameter is equal to
-step conjecture, asserts that the diameter is equal to  if the polytope has precisely
if the polytope has precisely 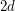 facets. The
facets. The  -step conjecture has been verified for
-step conjecture has been verified for 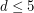 , and similarly as the Hirsch Conjecture, it is completely open for higher dimensions. This has been the situation for the past 50 years, and there is no evidence for essential progress.
, and similarly as the Hirsch Conjecture, it is completely open for higher dimensions. This has been the situation for the past 50 years, and there is no evidence for essential progress.
Bibliography
*[D] G. B. Dantzig: Linear Programming and Extensions, Princeton University Press (1963).
[KK] G. Kalai and D. J. Kleitman, A quasi-polynomial bound for the diameter of graphs of polyhedra, Bull. Amer. Math. Soc. (N.S.) 26 (1992), 315-316.
[MT] T. Matsui and S. Tamura, Adjacency on combinatorial polyhedra, Discrete Appl. Math. 56 (1995) 311-321.
[N] D. Naddef, The Hirsch conjecture is true for (0,1)-polytopes, Math. Progr. (Ser. B) 45 (1989) 109-110.
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.
there are someone who's working on it...
http://www.readwriteweb.com/archives/the_hirsch_conjecture_disproved.php
<< Santos, Francisco (University of Cantabria, Spain) A counter-example to the Hirsch conjecture
Victor Klee came to the Department of Mathematics to talk to me. We had a nice conversation during which he asked "Why don't you try to disprove the Hirsch Conjecture?" This talk is the answer to that question.
I will describe the construction of a 43-dimensional polytope with 86 facets and diameter bigger than 43. The proof is based on a generalization of the  -step theorem of Klee and Walkup. >>
-step theorem of Klee and Walkup. >>
copy paste from: https://sites.google.com/a/alaska.edu/kleegrunbaum/home/abstracts#Santos
best regards.
J.R.!
Settled
This conjecture has been settled in the negative by Francisco Santos.
Thats what i thought
Is there a difference from the negative to the positive? renters insurance quotes

 be a convex
be a convex 
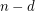 .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University
Santos arXiv paper
Here is Santos's arXiv paper with the counterexample: http://arxiv.org/abs/1006.2814. --Joseph O'Rourke