 login/create account
login/create account
Cube-Simplex conjecture
 , there exists an integer
, there exists an integer  so that every polytope of dimension
so that every polytope of dimension 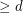 has a
has a  -dimensional face which is either a simplex or is combinatorially isomorphic to a
-dimensional face which is either a simplex or is combinatorially isomorphic to a  -dimensional cube.
-dimensional cube. It is an easy consequence of Euler's formula that every 3-polytope has a face which is either a triangle, a quadrilateral, or a pentagon. The 120-cell is a 4-polytope in which every 2-face is a pentagon (in fact every 3-face is a regular dodecahedron). Perles and Shephard asked whether there exist higher dimensional polytopes in which all 2-faces have at least 5 vertices. This question was answered in the negative by Kalai [K] who showed that every 5-polytope has a 2-face with at most 4 vertices. So, if we define 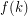 to be the smallest integer
to be the smallest integer  satisfying the above conjecture for
satisfying the above conjecture for  , or
, or 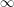 if none exists, then
if none exists, then 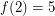 .
.
This conjecture is still open for simple polytopes. However, it is known that for every positive integer  , there exists an integer
, there exists an integer  so that every simple polytope of dimension
so that every simple polytope of dimension 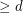 either has a 2-dimensional face which is a triangle, or a
either has a 2-dimensional face which is a triangle, or a  -dimensional face which is combinatorially isomorphic to a cube. This was proved by Kalai [K] using some earlier results of Nikulin and of Blind and Blind. Actually, something much stronger holds here: simple polytopes of sufficiently high dimension without 2-faces which are triangles must have most
-dimensional face which is combinatorially isomorphic to a cube. This was proved by Kalai [K] using some earlier results of Nikulin and of Blind and Blind. Actually, something much stronger holds here: simple polytopes of sufficiently high dimension without 2-faces which are triangles must have most  -dimensional faces combinatorially isomorphic to the
-dimensional faces combinatorially isomorphic to the  -cube.
-cube.
The following is an interesting weakening of the above conjecture.
 , there exists an integer
, there exists an integer  and a finite list
and a finite list 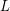 of
of  -dimensional polytopes, so that every polytope of dimension
-dimensional polytopes, so that every polytope of dimension 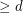 has a
has a  -dimensional face which appears in
-dimensional face which appears in 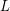 .
. Defining 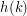 to be the smallest integer
to be the smallest integer  satisfying this conjecture for
satisfying this conjecture for  , or
, or 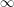 if none exists, we find that
if none exists, we find that 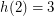 (by the consequence of Euler's formula in the first paragraph). Meisinger, Kleinschmidt, and Kalai [MKK] proved that
(by the consequence of Euler's formula in the first paragraph). Meisinger, Kleinschmidt, and Kalai [MKK] proved that 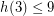 with the help of FLAGTOOL, a computer program which can compute linear relations for
with the help of FLAGTOOL, a computer program which can compute linear relations for 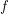 -vectors. This weaker conjecture is known to be true for simple polytopes.
-vectors. This weaker conjecture is known to be true for simple polytopes.
Bibliography
[MKK] G. Meisinger, P. Kleinschmidt, and G. Kalai, Three theorems, with computer-aided proofs, on three-dimensional faces and quotients of polytopes. The Branko Grünbaum birthday issue. Discrete Comput. Geom. 24 (2000), no. 2-3, 413--420. MathSciNet
*[K] G. Kalai, On low-dimensional faces that high-dimensional polytopes must have. Combinatorica 10 (1990), no. 3, 271--280. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University