Home » Author index

Hurtado, Ferran


Geometry

Chromatic number of associahedron ★★

Author(s): Fabila-Monroy; Flores-Penaloza; Huemer; Hurtado; Urrutia; Wood

Conjecture   Associahedra have unbounded chromatic number.

Keywords: associahedron, graph colouring, chromatic number

Posted by David Wood
updated June 2nd, 2015
add new comment
Geometry

Edge-Colouring Geometric Complete Graphs ★★

Author(s): Hurtado

Question   What is the minimum number of colours such that every complete geometric graph on $ n $ vertices has an edge colouring such that:
    \item[Variant A] crossing edges get distinct colours, \item[Variant B] disjoint edges get distinct colours, \item[Variant C] non-disjoint edges get distinct colours, \item[Variant D] non-crossing edges get distinct colours.

Keywords: geometric complete graph, colouring

Posted by David Wood
updated October 19th, 2009
add new comment
Graph Theory » Topological G.T. » Coloring

3-Colourability of Arrangements of Great Circles ★★

Author(s): Felsner; Hurtado; Noy; Streinu

Consider a set 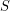$ S $ of great circles on a sphere with no three circles meeting at a point. The arrangement graph of 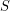$ S $ has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.

Conjecture   Every arrangement graph of a set of great circles is 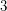$ 3 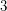$-colourable.

Keywords: arrangement graph; graph coloring

Posted by David Wood
updated October 22nd, 2020
2 comments
Syndicate content