 login/create account
login/create account
Noy, Marc
3-Colourability of Arrangements of Great Circles ★★
Author(s): Felsner; Hurtado; Noy; Streinu
Consider a set 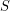 of great circles on a sphere with no three circles meeting at a point. The arrangement graph of
of great circles on a sphere with no three circles meeting at a point. The arrangement graph of 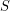 has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
has a vertex for each intersection point, and an edge for each arc directly connecting two intersection points. So this arrangement graph is 4-regular and planar.
Conjecture Every arrangement graph of a set of great circles is 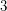 -colourable.
-colourable.
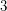 -colourable.
-colourable. Keywords: arrangement graph; graph coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University