 login/create account
login/create account
Edge-Colouring Geometric Complete Graphs
 vertices has an edge colouring such that:
vertices has an edge colouring such that:- \item[Variant A] crossing edges get distinct colours, \item[Variant B] disjoint edges get distinct colours, \item[Variant C] non-disjoint edges get distinct colours, \item[Variant D] non-crossing edges get distinct colours.
Let  be a set of
be a set of  points in the plane with no three collinear. Draw a straight line-segment between each pair of points in
points in the plane with no three collinear. Draw a straight line-segment between each pair of points in  . We obtain the complete geometric graph with vertex set
. We obtain the complete geometric graph with vertex set  , denoted by
, denoted by 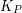 .
.
Two edges in 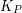 are either:
are either:
- \item adjacent if they have a vertex in common, \item crossing if they intersect at a point in the interior of both edges. \item disjoint if they do not intersect.
Let 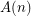 ,
, 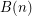 ,
, 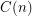 and
and 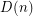 be the minimum number of colours for the four variants.
be the minimum number of colours for the four variants.
Variant A: Here each colour class is a plane subgraph. Since there are point sets for which 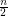 edges are pairwise crossing,
edges are pairwise crossing, 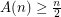 . For an upper bound, say
. For an upper bound, say 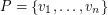 . Colour each edge
. Colour each edge 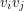 with
with 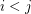 by colour
by colour  . Each colour class is a non-crossing star. So
. Each colour class is a non-crossing star. So 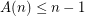 . Bose et al [BHRW] improved this upper bound to
. Bose et al [BHRW] improved this upper bound to 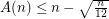 .
.
Conjecture. 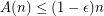 for some
for some  .
.
Variant B: Here edges receiving the same colour must intersect. So each colour class is a geometric thrackle. Since there are point sets for which 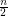 edges are pairwise disjoint,
edges are pairwise disjoint, 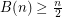 . The
. The 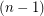 -colouring given in Variant A also works here. So
-colouring given in Variant A also works here. So 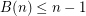 .
.
Conjecture. 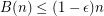 for some
for some  .
.
Variant C: Here each colour class is a plane matching. So each colour class has at most 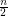 edges, and thus at least
edges, and thus at least 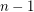 colours are always needed. Thus
colours are always needed. Thus 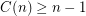 . Araujo [ADHNU] proved an upper bound of
. Araujo [ADHNU] proved an upper bound of 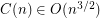 .
.
Conjecture. 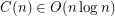 .
.
Strong Conjecture.  .
.
Variant D: (This variant was recently mentioned in [Mat].) Here edges receiving the same colour must cross. Each colour class is called a crossing family [ADHNU]. Every edge in any triangulation of  requires its own colour. So if the convex hull of
requires its own colour. So if the convex hull of  has only three points, then at least
has only three points, then at least 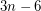 colours are needed. Thus
colours are needed. Thus 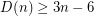 .
.
Conjecture. A super-linear number of colours are always needed; i.e., 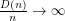 as
as 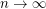 .
.
A better lower bound is obtained by taking  in convex position. Then
in convex position. Then 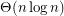 is the minimum number of colours [KK]. I am not aware of any non-trivial upper bound for arbitrary point sets
is the minimum number of colours [KK]. I am not aware of any non-trivial upper bound for arbitrary point sets  .
.
Bibliography
[ADHNU] G. Araujo, A. Dumitrescu, F. Hurtado, M. Noy, J. Urrutia, On the chromatic number of some geometric type Kneser graphs, Computational Geometry: Theory & Applications 32(1):59–69, 2005 MathSciNet
[BHRW] Prosenjit Bose, Ferran Hurtado, Eduardo Rivera-Campo, David R. Wood. Partitions of complete geometric graphs into plane trees, Computational Geometry: Theory & Applications 34(2):116-125, 2006. MathSciNet
[AEGKKPS] B. Aronov, P. Erdos, W. Goddard, D.J. Kleitman, M. Klugerman, J. Pach, L.J. Schulman, Crossing families, Combinatorica 14(2):127–134, 1994. MathSciNet
[KK] Alexandr Kostochka and Jan Kratochvil. Covering and coloring polygon-circle graphs, Discrete Math. 163(1--3):299--305, 1997. MathSciNet
[Mat] Jiří Matoušek. Blocking visibility for points in general position. Discrete Comput. Geom. 42(2):219--223, 2009. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University