 login/create account
login/create account
Sum of prime and semiprime conjecture
Conjecture Every even number greater than 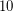 can be represented as the sum of an odd prime number and an odd semiprime .
can be represented as the sum of an odd prime number and an odd semiprime .
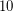 can be represented as the sum of an odd prime number and an odd semiprime .
can be represented as the sum of an odd prime number and an odd semiprime . Bibliography
*[M] Geoffrey R. Marnell, "Ten Prime Conjectures", Journal of Recreational Mathematics 33:3 (2004-2005), pp. 193--196.
* indicates original appearance(s) of problem.
Yes, apart from the
On July 31st, 2016 Charles R Great... says:
Yes, apart from the "sufficiently large" and allowing prime + prime as well as prime + semiprime. The parity problem makes the latter hard, but some progress has been made, see arXiv:math/0609615 and arXiv:0803.2636. (The key progress is their use of E2 = semiprimes rather than P2 = primes or semiprimes.)

 Drupal
Drupal CSI of Charles University
CSI of Charles University
surely that's Chen's theorem
Every sufficiently large even number is the sum of either 2 primes or a prime and a semiprime.