 login/create account
login/create account
outward reloid
Outward reloid of composition vs composition of outward reloids ★★
Author(s): Porton
Conjecture For every composable funcoids  and
and 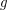
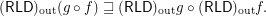
 and
and 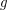
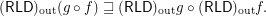
Keywords: outward reloid
Reloid corresponding to funcoid is between outward and inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; outward reloid; reloid
Outward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; outward reloid; reloid
Distributivity of outward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; outward reloid; reloid

![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
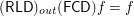 for any
for any 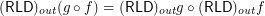 for any composable
for any composable  Drupal
Drupal CSI of Charles University
CSI of Charles University