 login/create account
login/create account
reloid
Direct proof of a theorem about compact funcoids ★★
Author(s): Porton
 is a
is a 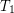 -separable (the same as
-separable (the same as 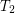 for symmetric transitive) compact funcoid and
for symmetric transitive) compact funcoid and 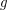 is a uniform space (reflexive, symmetric, and transitive endoreloid) such that
is a uniform space (reflexive, symmetric, and transitive endoreloid) such that 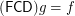 . Then
. Then 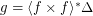 .
. The main purpose here is to find a direct proof of this conjecture. It seems that this conjecture can be derived from the well known theorem about existence of exactly one uniformity on a compact set. But that would be what I call an indirect proof, we need a direct proof instead.
The direct proof may be constructed by correcting all errors an omissions in this draft article.
Direct proof could be better because with it we would get a little more general statement like this:
 be a
be a 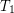 -separable compact reflexive symmetric funcoid and
-separable compact reflexive symmetric funcoid and 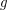 be a reloid such that
be a reloid such that- \item
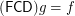 ; \item
; \item 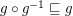 .
. Then 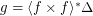 .
.
Keywords: compact space; compact topology; funcoid; reloid; uniform space; uniformity
Decomposition of completions of reloids ★★
Author(s): Porton
 and
and 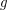 it holds
it holds- \item
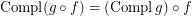 if
if  is a co-complete reloid; \item
is a co-complete reloid; \item 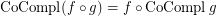 if
if  is a complete reloid; \item
is a complete reloid; \item 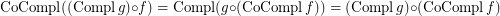 ; \item
; \item 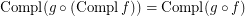 ; \item
; \item 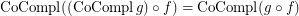 .
. Keywords: co-completion; completion; reloid
Distributivity of inward reloid over composition of funcoids ★★
Author(s): Porton
Keywords: distributive; distributivity; funcoid; functor; inward reloid; reloid
Atomic reloids are monovalued ★★
Author(s): Porton
Keywords: atomic reloid; monovalued reloid; reloid
Composition of atomic reloids ★★
Author(s): Porton
Keywords: atomic reloid; reloid
Reloid corresponding to funcoid is between outward and inward reloid ★★
Author(s): Porton
Keywords: funcoid; inward reloid; outward reloid; reloid
Distributivity of union of funcoids corresponding to reloids ★★
Author(s): Porton
Keywords: funcoid; infinite distributivity; reloid
Inward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; inward reloid; reloid
Outward reloid corresponding to a funcoid corresponding to convex reloid ★★
Author(s): Porton
Keywords: convex reloid; funcoid; functor; outward reloid; reloid

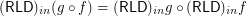 for any composable
for any composable 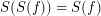 for every endo-
for every endo-![\[ ( \mathsf{\tmop{RLD}})_{\tmop{out}} f \subseteq g \subseteq ( \mathsf{\tmop{RLD}})_{\tmop{in}} f \Leftrightarrow ( \mathsf{\tmop{FCD}}) g = f. \]](/files/tex/def032a20d7d57db67d77c0f002f1c9f2909fe98.png)
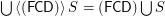 if
if 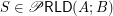 is a set of
is a set of 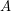 to a set
to a set 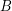 .
. 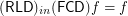 for any
for any 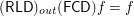 for any
for any  Drupal
Drupal CSI of Charles University
CSI of Charles University