 login/create account
login/create account
Decomposition of completions of reloids
Conjecture For composable reloids  and
and 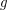 it holds
it holds
 and
and 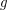 it holds
it holds- \item
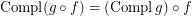 if
if  is a co-complete reloid; \item
is a co-complete reloid; \item 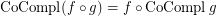 if
if  is a complete reloid; \item
is a complete reloid; \item 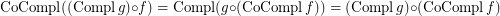 ; \item
; \item 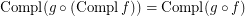 ; \item
; \item 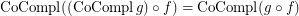 .
. Well, in fact this is three separate problems (if we count dual formulas as one formula), but I am lazy to create three pages for them.
This conjecture is inspired by the proven fact that the above formulas hold for every composable funcoids  and
and 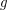 (instead of reloids). Properties of reloids are expected to be similar to properties of funcoids.
(instead of reloids). Properties of reloids are expected to be similar to properties of funcoids.
http://www.packersandmoverschandigarh.co.in/
http://www.packersandmoversjaipur.co.in/
http://www.packersandmoversinhyderabad.co.in/
http://www.packersandmoversinbangalore.co.in/
Bibliography
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University