 login/create account
login/create account
 -flow for some
-flow for some  , has a nowhere-zero
, has a nowhere-zero  -flow.
-flow. Definition: A bidirected graph is a graph in which every edge has two arrowheads, one next to each endpoint. If the edge  has ends
has ends  and
and  , then the arrowheads nearest
, then the arrowheads nearest  and
and  may point either toward
may point either toward  or toward
or toward  (giving four possibilities in all). If
(giving four possibilities in all). If  is a bidirected graph, a
is a bidirected graph, a  -flow of G is a map
-flow of G is a map 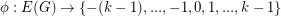 with the property that at every vertex, the sum of
with the property that at every vertex, the sum of 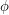 on the edges whose ends at
on the edges whose ends at  are directed into
are directed into  is equal to the sum of
is equal to the sum of 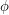 on the edges whose ends at
on the edges whose ends at  are directed out of
are directed out of  . We say that
. We say that 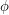 is nowhere-zero if
is nowhere-zero if 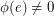 for every
for every  (see nowhere-zero flows).
(see nowhere-zero flows).

Flows on bidirected graphs arise naturally as duals of local-tensions on a non-orientable surface. For more on this relationship, see [B]. Bouchet proved that the above conjecture is true with 6 replaced by 216, and exhibited a bidirected Petersen graph as above which shows that 6 is the best value possible. Zyka [Z] and independently Fouquet improved upon this result proving that the above conjecture is true with 6 replaced by 30. Khelladi [K] proved that for 4-connected graphs, the above conjecture is true with 6 replaced by 18. DeVos [D] proved that the above conjecture holds with 6 replaced by 12, and showed that every 4-edge-connected bidirected graph with a nowhere-zero integer flow also has a nowhere-zero 4-flow.
Bibliography
[B] A. Bouchet, Nowhere-Zero Integral Flows on a Bidirected Graph, J. Combinatorial Theory Ser. B 34 (1983) 279-292. MathSciNet
[D] M. DeVos, Flows on Bidirected Graphs, preprint.
[K] A. Khelladi, Nowhere-Zero Integral Chains and Flows in Bidirected Graphs, J. Combinatorial Theory Ser. B 43 (1987) 95-115. MathSciNet
[Z] O. Zyka, Bidirected Nowhere-Zero Flows, Thesis, Charles University, Praha (1988).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University