 login/create account
login/create account
Ancient/folklore
Fundamental group torsion for subsets of Euclidean 3-space ★★
Author(s): Ancient/folklore
Problem Does there exist a subset of 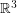 such that its fundamental group has an element of finite order?
such that its fundamental group has an element of finite order?
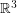 such that its fundamental group has an element of finite order?
such that its fundamental group has an element of finite order?
Keywords: subsets of euclidean space; torsion
Which homology 3-spheres bound homology 4-balls? ★★★★
Author(s): Ancient/folklore
Problem Is there a complete and computable set of invariants that can determine which (rational) homology  -spheres bound (rational) homology
-spheres bound (rational) homology  -balls?
-balls?
 -spheres bound (rational) homology
-spheres bound (rational) homology  -balls?
-balls?
Keywords: cobordism; homology ball; homology sphere
Odd perfect numbers ★★★
Author(s): Ancient/folklore
Conjecture There is no odd perfect number.
Keywords: perfect number

 Drupal
Drupal CSI of Charles University
CSI of Charles University