 login/create account
login/create account
Fundamental group torsion for subsets of Euclidean 3-space
Problem Does there exist a subset of 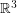 such that its fundamental group has an element of finite order?
such that its fundamental group has an element of finite order?
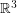 such that its fundamental group has an element of finite order?
such that its fundamental group has an element of finite order?
The corresponding problem in 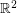 has a negative answer. The corresponding problem in
has a negative answer. The corresponding problem in 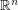 for
for 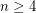 has a positive answer. If the subset of
has a positive answer. If the subset of 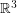 has a regular neighbourhood with a smooth boundary, the answer is negative. Similarly the homology of the subset is known to have no torsion via an Alexander duality argument. So any torsion in the fundamental group must be in the commutator subgroup.
has a regular neighbourhood with a smooth boundary, the answer is negative. Similarly the homology of the subset is known to have no torsion via an Alexander duality argument. So any torsion in the fundamental group must be in the commutator subgroup.
Bibliography
[E] Eda, K. Fundamental group of subsets of the plane. Topology and its Applications Volume 84, Issues 1-3, 24 April 1998, Pages 283-306
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University