 login/create account
login/create account
Which homology 3-spheres bound homology 4-balls?
 -spheres bound (rational) homology
-spheres bound (rational) homology  -balls?
-balls?
Determining which homology  -spheres bound homology
-spheres bound homology  -balls is a long standing open problem in 3/4-manifold topology. Much effort has gone towards understanding the situation for the Brieskorn homology spheres. For example, the Poincare Dodecahedral space is known not to bound a homology
-balls is a long standing open problem in 3/4-manifold topology. Much effort has gone towards understanding the situation for the Brieskorn homology spheres. For example, the Poincare Dodecahedral space is known not to bound a homology  -ball since the Rochlin invariant is non-trivial -- but
-ball since the Rochlin invariant is non-trivial -- but 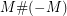 the connect-sum of Poincare Dodecahedral space
the connect-sum of Poincare Dodecahedral space  with its orientation-reverse does bound a homology 4-ball, and it has a simple construction: remove an open tubular neighbourhood of
with its orientation-reverse does bound a homology 4-ball, and it has a simple construction: remove an open tubular neighbourhood of 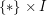 from
from 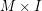 , this is the
, this is the  -manifold.
-manifold.
Standard invariants used to show homology  -spheres do not bound homology
-spheres do not bound homology  -balls are various spin or spin^c cobordism invariants such as: the Rochlin invariant, Siebenmann's
-balls are various spin or spin^c cobordism invariants such as: the Rochlin invariant, Siebenmann's 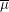 -invariant, the Oszvath-Szabo
-invariant, the Oszvath-Szabo  -invariant, and there are many others.
-invariant, and there are many others.
Bibliography
[K] Kirby, Robion (1989), The topology of 4-manifolds, Lecture Notes in Mathematics, 1374, Springer-Verlag,
[R] Rokhlin, Vladimir A, New results in the theory of four-dimensional manifolds, Doklady Acad. Nauk. SSSR (N.S.) 84 (1952) 221-224.
[AK] S.Akbulut, R.Kirby, "Mazur manifolds," Michigan Math. J. 26 (1979), 259--284.
[CH] A.Casson, J.Harer, "Some homology lens spaces which bound rational homology balls." Pacific. J. Math. Vol 96, No 1, (1981) 23–36.
[F] H.Fickle, "Knots, Z-Homology 3-spheres and contractible 4-manifolds," pp. 467--493, Houston J. Math. Vol 10, No. 4 (1984).
[FS] R.Fintushel, R.Stern, "An exotic free involution on S^4," Ann. Math. (2) 113 (1981) no2, 357--365.
[M] B.Mazur, "A note on some contractible 4-manifolds", Annals of Mathematics, (2) 73 (1961). 221–228.
[S] R.Stern,"Some Brieskorn spheres which bound contractible manifolds," Notices Amer. Math. Soc 25 (1978), A448.
[L] Lisca, Paolo Sums of lens spaces bounding rational balls. Algebr. Geom. Topol. 7 (2007), 2141--2164.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University