 login/create account
login/create account
Slice-ribbon problem
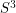 which is slice, is it a ribbon knot?
which is slice, is it a ribbon knot?
The definitions of slice and ribbon: slice knot ribbon knot
There is a fairly vast literature on this problem. It is closely related to the problem of determining which homology  -spheres bound homology
-spheres bound homology  -balls, as both are in essence a type of
-balls, as both are in essence a type of  -dimensional cobordism problem.
-dimensional cobordism problem.
Bibliography
*[F] Fox, R. H. Some problems in knot theory. 1962 Topology of 3-manifolds and related topics (Proc. The Univ. of Georgia Institute, 1961) pp. 168--176
[G] Gilmer, Patrick M. On the slice genus of knots. Invent. Math. 66 (1982), no. 2, 191--197.
[H] Hass, Joel. The geometry of the slice-ribbon problem. Math. Proc. Cambridge Philos. Soc. 94 (1983), no. 1, 101--108.
Ana G. Lecuona. [arXiv:0910.4601] On the Slice-Ribbon Conjecture for Montesinos knots
Brendan Owens. [arXiv:0802.2109] On slicing invariants of knots.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University