 login/create account
login/create account
Odd cycles and low oddness
 the cycles of any
the cycles of any  -factor are odd, then
-factor are odd, then 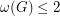 , where
, where 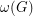 denotes the oddness of the graph
denotes the oddness of the graph  , that is, the minimum number of odd cycles in a
, that is, the minimum number of odd cycles in a  -factor of
-factor of  .
. This conecture is false.
Case 2: If all of the edges of the form 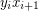 are contained in the same cycle in a 2-factor of
are contained in the same cycle in a 2-factor of 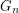 , then replacing the edges
, then replacing the edges 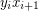 with the edges
with the edges 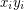 converts this 2-factor of
converts this 2-factor of 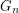 into a 2-factor of
into a 2-factor of  disjoint copies of the Petersen graph. Hence, when restricted to each
disjoint copies of the Petersen graph. Hence, when restricted to each 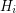 , the 2-factor of
, the 2-factor of 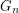 consists of a cycle with 5 vertices and a
consists of a cycle with 5 vertices and a 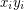 -path containing a total of 5 vertices. These paths must be joined together through the edges of the form
-path containing a total of 5 vertices. These paths must be joined together through the edges of the form 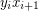 creating a cycle of length 5n. Hence, in this case the 2-factor of
creating a cycle of length 5n. Hence, in this case the 2-factor of 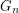 contains
contains  cycles of length 5 and one cycle of length 5n (which is odd).
cycles of length 5 and one cycle of length 5n (which is odd).
Now, 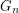 is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of
is a bridgeless cubic graph whose 2-factors contain only odd cycles, but no 2-factor of 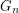 contains fewer than
contains fewer than 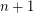 cycles.
cycles.
what is oddness
The notion of oddness of a graph requires explanation.
Let be a bridgeless cubic
Let  be a bridgeless cubic graph. The oddness of a 2-factor
be a bridgeless cubic graph. The oddness of a 2-factor 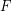 is the number of odd circuits of
is the number of odd circuits of 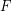 . The oddness of
. The oddness of  is the smallest oddness over all 2-factors. For example, a 3-edge-colorable cubic graph has oddness zero and the Petersen graph has oddness two.
is the smallest oddness over all 2-factors. For example, a 3-edge-colorable cubic graph has oddness zero and the Petersen graph has oddness two.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
This conjecture is false.
For odd and
and ![$ i\in[n] $](/files/tex/3489ac3673ff1a2165798412b5aaf3c992a55253.png) , let
, let 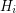 be the graph obtained by deleting an edge, say
be the graph obtained by deleting an edge, say 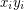 , from the Petersen graph. Define
, from the Petersen graph. Define 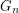 to be the graph obtained by joining vertex
to be the graph obtained by joining vertex 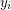 and vertex
and vertex 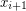 with an edge (with subscripts reduced modulo
with an edge (with subscripts reduced modulo  ). For each
). For each ![$ i\in[n] $](/files/tex/3489ac3673ff1a2165798412b5aaf3c992a55253.png) , the set
, the set 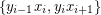 is an edge cut. Hence, in any 2-factor of
is an edge cut. Hence, in any 2-factor of 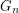 , either none of the edges of the form
, either none of the edges of the form 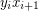 are contained in a cycle, or all of them are contained in the same cycle.
are contained in a cycle, or all of them are contained in the same cycle.
Case 1: If none of the edges described above are contained in a cycle of a 2-factor of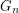 , then this 2-factor contains a 2-factor of
, then this 2-factor contains a 2-factor of 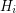 for each
for each  . These 2-factors are also 2-factors of the graphs
. These 2-factors are also 2-factors of the graphs 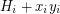 , that is, each is a 2-factor of the Petersen graph. Each 2-factor of the Petersen graph consists of two cycles of 5 vertices, hence, any such 2-factor of
, that is, each is a 2-factor of the Petersen graph. Each 2-factor of the Petersen graph consists of two cycles of 5 vertices, hence, any such 2-factor of 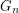 contains
contains 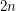 cycles of odd length.
cycles of odd length.
Case 2: See the comment below.