 login/create account
login/create account
Sequence defined on multisets
Conjecture Define a 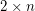 array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array
array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) , the sequence is:
, the sequence is: ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) ->
-> ![$ [1; 2] $](/files/tex/83c3d9d7589f716ed6b0f05d26d36dabe8ba47aa.png) ->
-> ![$ [1, 2; 1, 1] $](/files/tex/a6a696aec4e84df6bc046cf6d30a4df80e156a14.png) ->
-> ![$ [1, 2; 3, 1] $](/files/tex/98b2f3e4134422c8a286f0326fc2f57ca9be2ab7.png) ->
-> ![$ [1, 2, 3; 2, 1, 1] $](/files/tex/19a9d24510f4551fa45b950aed32efed0636b355.png) ->
-> ![$ [1, 2, 3; 3, 2, 1] $](/files/tex/b00d573110ba8c2472820409103dd4cbd7bff7cc.png) ->
-> ![$ [1, 2, 3; 2, 2, 2] $](/files/tex/2aae90b65ae3f116402a1c0143127f80d86acdf0.png) ->
-> ![$ [1, 2, 3; 1, 4, 1] $](/files/tex/d614399c4078a70fbffb24eb99816a0974423175.png) ->
-> ![$ [1, 2, 3, 4; 3, 1, 1, 1] $](/files/tex/bf4dd82eaf95bd71a88cb78d3367efa2c7e4c942.png) ->
-> ![$ [1, 2, 3, 4; 4, 1, 2, 1] $](/files/tex/a4ef5900a9dde9b32311afe7dee2b143f42c405f.png) ->
-> ![$ [1, 2, 3, 4; 3, 2, 1, 2] $](/files/tex/ff367376ed7bb74fc6207273d7157062b83a1be6.png) ->
-> ![$ [1, 2, 3, 4; 2, 3, 2, 1] $](/files/tex/81ba2b3608ddba2fc95d32b74b70279f3f5adc5b.png) , and we now have a fixed point (loop of one array).
, and we now have a fixed point (loop of one array).
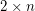 array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array
array of positive integers where the first row consists of some distinct positive integers arranged in increasing order, and the second row consists of any positive integers in any order. Create a new array where the first row consists of all the integers that occur in the first array, arranged in increasing order, and the second row consists of their multiplicities. Repeat the process. For example, starting with the array ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) , the sequence is:
, the sequence is: ![$ [1; 1] $](/files/tex/73f8649de444361674c157a2fe98e0c5783f1c46.png) ->
-> ![$ [1; 2] $](/files/tex/83c3d9d7589f716ed6b0f05d26d36dabe8ba47aa.png) ->
-> ![$ [1, 2; 1, 1] $](/files/tex/a6a696aec4e84df6bc046cf6d30a4df80e156a14.png) ->
-> ![$ [1, 2; 3, 1] $](/files/tex/98b2f3e4134422c8a286f0326fc2f57ca9be2ab7.png) ->
-> ![$ [1, 2, 3; 2, 1, 1] $](/files/tex/19a9d24510f4551fa45b950aed32efed0636b355.png) ->
-> ![$ [1, 2, 3; 3, 2, 1] $](/files/tex/b00d573110ba8c2472820409103dd4cbd7bff7cc.png) ->
-> ![$ [1, 2, 3; 2, 2, 2] $](/files/tex/2aae90b65ae3f116402a1c0143127f80d86acdf0.png) ->
-> ![$ [1, 2, 3; 1, 4, 1] $](/files/tex/d614399c4078a70fbffb24eb99816a0974423175.png) ->
-> ![$ [1, 2, 3, 4; 3, 1, 1, 1] $](/files/tex/bf4dd82eaf95bd71a88cb78d3367efa2c7e4c942.png) ->
-> ![$ [1, 2, 3, 4; 4, 1, 2, 1] $](/files/tex/a4ef5900a9dde9b32311afe7dee2b143f42c405f.png) ->
-> ![$ [1, 2, 3, 4; 3, 2, 1, 2] $](/files/tex/ff367376ed7bb74fc6207273d7157062b83a1be6.png) ->
-> ![$ [1, 2, 3, 4; 2, 3, 2, 1] $](/files/tex/81ba2b3608ddba2fc95d32b74b70279f3f5adc5b.png) , and we now have a fixed point (loop of one array).
, and we now have a fixed point (loop of one array).
The process always results in a loop of 1, 2, or 3 arrays.
Bibliography
* Erickson, Martin J., "Introduction to Combinatorics," Wiley, 1996.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Solution
This problem has recently been solved by the author.