 login/create account
login/create account
Twin prime conjecture
 so that both
so that both  and
and 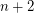 are prime.
are prime.
Bibliography
* indicates original appearance(s) of problem.
Regarding the Tyte's proof I
Regarding the Tyte's proof I have received three enthusiastic comments-contributions, pointing out that while the averaging step made by Alan is questionable, maybe this approach shows where to look for in the solution of this Conjecture. These first three comments are from Chris Nash, Fabrice Marchant and Leadhyena Inrandomtan:
"About Alan Tyte's proof : all the beginning up to "Lemma 5" is right but there are 2 errors in the end of the proof, after each "Hence, on the average :" because we do not know the way our beloved Ds are spanned : no reason to be sure they are put at the same rate between x and x^2 than between a whole pattern. However, I think the idea of the proof with As, Bs ... is great and I'll try to work in the way of Alan." (F. Marchant)
Where is the conjecture?
The conjecture is not stated. It's just the definition.
I've added a thread here,
I've added a thread here, linking to an attempted proof of Twin Primes and the Polignac conjecture in general.
http://garden.irmacs.sfu.ca/?q=op/twin_primes_and_polignacs_conjecture
Will receive any input, debunking etc gratefully.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Twin Prime Conjecture
Hello.
I see a reference to a proof called Tyte's proof but saw no details on it. When I click on the link, it only gives me the same page that I'm already on.
Also, I could not get any additional details about the following post:
On January 10th, 2011 Hugh Barker says: I've added a thread here, linking to an attempted proof of Twin Primes and the Polignac conjecture in general.
http://garden.irmacs.sfu.ca/?q=op/twin_primes_and_polignacs_conjecture
Will receive any input, debunking etc gratefully.
I am most interested in searching for any attempted proofs of the twin prime conjecture. I believe that I have a proof, but anticipate clearly filling in some details.
The core idea in our proof is that we specify exactly a lower bound for the number of twin primes less than a given integer, N, and that this lower bound goes to infinity as N goes to infinity.
Kermit