 login/create account
login/create account
Strict inequalities for products of filters
Conjecture 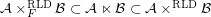 for some filter objects
for some filter objects 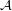 ,
, 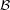 . Particularly, is this formula true for
. Particularly, is this formula true for 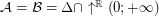 ?
?
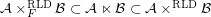 for some filter objects
for some filter objects 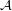 ,
, 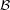 . Particularly, is this formula true for
. Particularly, is this formula true for 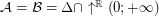 ?
? A weaker conjecture:
Conjecture 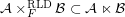 for some filter objects
for some filter objects 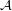 ,
, 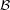 .
.
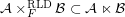 for some filter objects
for some filter objects 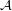 ,
, 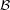 .
. See Algebraic General Topology for definitions of used concepts.
The first conjecture probably has no use by itself but proving it may be somehow challenging, just like Fermat Last Theorem.
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University