 login/create account
login/create account
ramsey theory
Multicolour Erdős--Hajnal Conjecture ★★★
Conjecture For every fixed 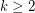 and fixed colouring
and fixed colouring 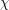 of
of 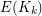 with
with  colours, there exists
colours, there exists 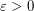 such that every colouring of the edges of
such that every colouring of the edges of 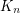 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 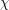 or
or 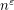 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 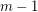 colours.
colours.
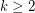 and fixed colouring
and fixed colouring 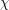 of
of 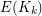 with
with  colours, there exists
colours, there exists 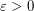 such that every colouring of the edges of
such that every colouring of the edges of 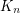 contains either
contains either  vertices whose edges are coloured according to
vertices whose edges are coloured according to 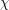 or
or 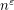 vertices whose edges are coloured with at most
vertices whose edges are coloured with at most 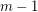 colours.
colours. Keywords: ramsey theory
Geometric Hales-Jewett Theorem ★★
Conjecture For all integers 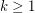 and
and 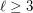 , there is an integer
, there is an integer 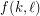 such that for every set
such that for every set  of at least
of at least 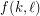 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:
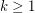 and
and 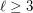 , there is an integer
, there is an integer 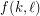 such that for every set
such that for every set  of at least
of at least 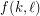 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:- \item
 contains
contains  collinear points, or \item
collinear points, or \item  contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour)
contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour) Keywords: Hales-Jewett Theorem; ramsey theory
Exact colorings of graphs ★★
Author(s): Erickson
Conjecture For 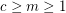 , let
, let 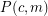 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 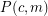 is true if and only if
is true if and only if 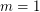 ,
, 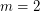 , or
, or  .
.
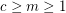 , let
, let 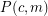 be the statement that given any exact
be the statement that given any exact  -coloring of the edges of a complete countably infinite graph (that is, a coloring with
-coloring of the edges of a complete countably infinite graph (that is, a coloring with  colors all of which must be used at least once), there exists an exactly
colors all of which must be used at least once), there exists an exactly  -colored countably infinite complete subgraph. Then
-colored countably infinite complete subgraph. Then 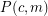 is true if and only if
is true if and only if 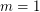 ,
, 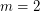 , or
, or  .
. Keywords: graph coloring; ramsey theory
Monochromatic empty triangles ★★★
Author(s):
If 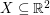 is a finite set of points which is 2-colored, an empty triangle is a set
is a finite set of points which is 2-colored, an empty triangle is a set 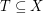 with
with 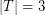 so that the convex hull of
so that the convex hull of  is disjoint from
is disjoint from  . We say that
. We say that  is monochromatic if all points in
is monochromatic if all points in  are the same color.
are the same color.
Conjecture There exists a fixed constant  with the following property. If
with the following property. If 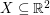 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 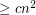 monochromatic empty triangles.
monochromatic empty triangles.
 with the following property. If
with the following property. If 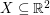 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 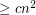 monochromatic empty triangles.
monochromatic empty triangles. Keywords: empty triangle; general position; ramsey theory
Erdös-Szekeres conjecture ★★★
Conjecture Every set of 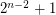 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon.
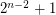 points in the plane in general position contains a subset of
points in the plane in general position contains a subset of  points which form a convex
points which form a convex  -gon.
-gon. Keywords: combinatorial geometry; Convex Polygons; ramsey theory

 Drupal
Drupal CSI of Charles University
CSI of Charles University