 login/create account
login/create account
Hales-Jewett Theorem
Geometric Hales-Jewett Theorem ★★
Conjecture For all integers 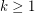 and
and 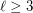 , there is an integer
, there is an integer 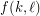 such that for every set
such that for every set  of at least
of at least 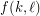 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:
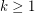 and
and 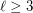 , there is an integer
, there is an integer 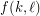 such that for every set
such that for every set  of at least
of at least 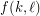 points in the plane, if each point in
points in the plane, if each point in  is assigned one of
is assigned one of  colours, then:
colours, then:- \item
 contains
contains 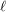 collinear points, or \item
collinear points, or \item  contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour)
contains a monochromatic line (that is, a maximal set of collinear points receiving the same colour) Keywords: Hales-Jewett Theorem; ramsey theory

 Drupal
Drupal CSI of Charles University
CSI of Charles University