Home » Subject » Geometry

Monochromatic empty triangles

Importance: High ✭✭✭
Author(s):
Subject: Geometry
Keywords: empty triangle
general position
ramsey theory
Recomm. for undergrads: no
Posted by: mdevos
on: October 8th, 2008

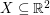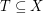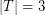If $ X \subseteq {\mathbb R}^2 $ is a finite set of points which is 2-colored, an empty triangle is a set $ T \subseteq X $ with $ |T|=3 $ so that the convex hull of $ T $ is disjoint from $ X \setminus T $. We say that $ T $ is monochromatic if all points in $ T $ are the same color.

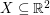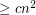Conjecture   There exists a fixed constant $ c $ with the following property. If $ X \subseteq {\mathbb R}^2 $ is a set of $ n $ points in general position which is 2-colored, then it has $ \ge cn^2 $ monochromatic empty triangles.

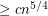It is known that any set of $ n $ points in the plane in general position contains $ \ge cn^{5/4} $ monochromatic empty triangles.

Bibliography



* indicates original appearance(s) of problem.
add new comment

This has a trivial

On September 27th, 2009 Anonymous says:

This has a trivial counterexample for c > 0.

Consider X = {(0,0), (0,1), (1,0)}, colored {red, blue, blue} respectively. There is only one empty triangle in X, and it is not monochromatic. So it has 0 monochromatic empty triangles, and 0 is not > c*(3^2) for c > 0.

reply

Yes indeed. However in this

On August 27th, 2010 Anonymous says:

Yes indeed. However in this types of problems it is generally implied that the statement is for a sufficently large n.

reply

Original source and one improvement.

On May 12th, 2009 Anonymous says:

The conjecture appeared first in "Oswin Aichholzer, Ruy Fabila-Monroy, David Flores-Peñaloza, Thomas Hackl, Clemens Huemer, and Jorge Urrutia. Empty monochromatic triangles. In Proceedings of the 20th Canadian Conference on Computational Geometry (CCCG2008), pages 75-78, 2008."

In this paper the authors show that any set of n points in general position has 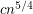$ cn^{5/4} $ empty monochromatic triangles. You can get this paper from http://cccg.ca/proceedings/2008/paper18.pdf

There is one improvement showing that any set of n points in general position has 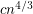$ cn^{4/3} $ empty monochromatic triangles in: "J. Pach, G. Toth. Monochromatic empty triangles in two-colored point sets. In: Geometry, Games, Graphs and Education: the Joe Malkevitch Festschrift (S. Garfunkel, R. Nath, eds.), COMAP, Bedford, MA, 2008, 195--198." Get it from: http://www.math.nyu.edu/~pach/publications/emptytriangle102408.pdf

reply

The lower bound has been improved

On May 8th, 2009 Anonymous says:

The lower bound has been improved to cn4/3.

J. Pach and G. Toth: Monochromatic empty triangles in two-colored point sets, in: Geometry, Games, Graphs and Education: the Joe Malkevitch Festschrift (S. Garfunkel, R. Nath, eds.), COMAP, Bedford, MA, 2008, 195--198.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.