The conjecture appeared first in "Oswin Aichholzer, Ruy Fabila-Monroy, David Flores-Peñaloza, Thomas Hackl, Clemens Huemer, and Jorge Urrutia. Empty monochromatic triangles. In Proceedings of the 20th Canadian Conference on Computational Geometry (CCCG2008), pages 75-78, 2008."
In this paper the authors show that any set of n points in general position has empty monochromatic triangles. You can get this paper from http://cccg.ca/proceedings/2008/paper18.pdf
There is one improvement showing that any set of n points in general position has empty monochromatic triangles in: "J. Pach, G. Toth. Monochromatic empty triangles in two-colored point sets. In: Geometry, Games, Graphs and Education: the Joe Malkevitch Festschrift (S. Garfunkel, R. Nath, eds.), COMAP, Bedford, MA, 2008, 195--198." Get it from: http://www.math.nyu.edu/~pach/publications/emptytriangle102408.pdf
Original source and one improvement.
The conjecture appeared first in "Oswin Aichholzer, Ruy Fabila-Monroy, David Flores-Peñaloza, Thomas Hackl, Clemens Huemer, and Jorge Urrutia. Empty monochromatic triangles. In Proceedings of the 20th Canadian Conference on Computational Geometry (CCCG2008), pages 75-78, 2008."
In this paper the authors show that any set of n points in general position has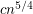 empty monochromatic triangles. You can get this paper from http://cccg.ca/proceedings/2008/paper18.pdf
empty monochromatic triangles. You can get this paper from http://cccg.ca/proceedings/2008/paper18.pdf
There is one improvement showing that any set of n points in general position has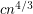 empty monochromatic triangles in: "J. Pach, G. Toth. Monochromatic empty triangles in two-colored point sets. In: Geometry, Games, Graphs and Education: the Joe Malkevitch Festschrift (S. Garfunkel, R. Nath, eds.), COMAP, Bedford, MA, 2008, 195--198." Get it from: http://www.math.nyu.edu/~pach/publications/emptytriangle102408.pdf
empty monochromatic triangles in: "J. Pach, G. Toth. Monochromatic empty triangles in two-colored point sets. In: Geometry, Games, Graphs and Education: the Joe Malkevitch Festschrift (S. Garfunkel, R. Nath, eds.), COMAP, Bedford, MA, 2008, 195--198." Get it from: http://www.math.nyu.edu/~pach/publications/emptytriangle102408.pdf