 login/create account
login/create account
general position
Monochromatic empty triangles ★★★
Author(s):
If 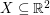 is a finite set of points which is 2-colored, an empty triangle is a set
is a finite set of points which is 2-colored, an empty triangle is a set 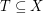 with
with 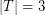 so that the convex hull of
so that the convex hull of  is disjoint from
is disjoint from  . We say that
. We say that  is monochromatic if all points in
is monochromatic if all points in  are the same color.
are the same color.
Conjecture There exists a fixed constant  with the following property. If
with the following property. If 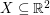 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 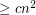 monochromatic empty triangles.
monochromatic empty triangles.
 with the following property. If
with the following property. If 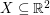 is a set of
is a set of  points in general position which is 2-colored, then it has
points in general position which is 2-colored, then it has 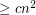 monochromatic empty triangles.
monochromatic empty triangles. Keywords: empty triangle; general position; ramsey theory

 Drupal
Drupal CSI of Charles University
CSI of Charles University