 login/create account
login/create account
funcoids
Entourages of a composition of funcoids ★★
Author(s): Porton
Conjecture 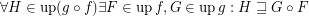 for every composable funcoids
for every composable funcoids  and
and 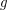 .
.
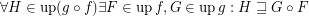 for every composable funcoids
for every composable funcoids  and
and 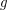 .
. Keywords: composition of funcoids; funcoids
Restricting a reloid to lattice Gamma before converting it into a funcoid ★★
Author(s): Porton
Conjecture 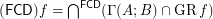 for every reloid
for every reloid 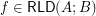 .
.
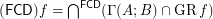 for every reloid
for every reloid 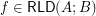 .
. Keywords: funcoid corresponding to reloid; funcoids; reloids
Inner reloid through the lattice Gamma ★★
Author(s): Porton
Conjecture 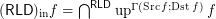 for every funcoid
for every funcoid  .
.
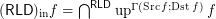 for every funcoid
for every funcoid  .
. Counter-example: 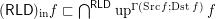 for the funcoid
for the funcoid 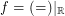 is proved in this online article.
is proved in this online article.
Keywords: filters; funcoids; inner reloid; reloids
Coatoms of the lattice of funcoids ★
Author(s): Porton
Problem Let 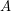 and
and 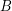 be infinite sets. Characterize the set of all coatoms of the lattice
be infinite sets. Characterize the set of all coatoms of the lattice 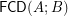 of funcoids from
of funcoids from 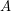 to
to 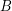 . Particularly, is this set empty? Is
. Particularly, is this set empty? Is 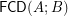 a coatomic lattice? coatomistic lattice?
a coatomic lattice? coatomistic lattice?
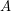 and
and 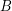 be infinite sets. Characterize the set of all coatoms of the lattice
be infinite sets. Characterize the set of all coatoms of the lattice 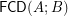 of funcoids from
of funcoids from 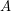 to
to 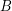 . Particularly, is this set empty? Is
. Particularly, is this set empty? Is 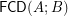 a coatomic lattice? coatomistic lattice?
a coatomic lattice? coatomistic lattice? 
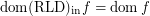 and
and 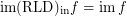 for every funcoid
for every funcoid  Drupal
Drupal CSI of Charles University
CSI of Charles University