 login/create account
login/create account
Conjecture 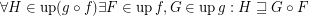 for every composable funcoids
for every composable funcoids  and
and  .
.
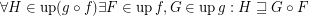 for every composable funcoids
for every composable funcoids  and
and  .
. There is now a counterexample in Algebraic General Topology book.
Bibliography
*Victor Porton. A blog post
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University