 login/create account
login/create account
filters
Inner reloid through the lattice Gamma ★★
Author(s): Porton
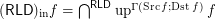 for every funcoid
for every funcoid  .
. Counter-example: 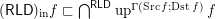 for the funcoid
for the funcoid 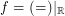 is proved in this online article.
is proved in this online article.
Keywords: filters; funcoids; inner reloid; reloids
Chain-meet-closed sets ★★
Author(s): Porton
Let 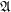 is a complete lattice. I will call a filter base a nonempty subset
is a complete lattice. I will call a filter base a nonempty subset  of
of 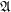 such that
such that 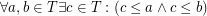 .
.
 of a complete lattice
of a complete lattice 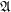 is chain-meet-closed iff for every non-empty chain
is chain-meet-closed iff for every non-empty chain 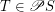 we have
we have 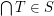 .
.  of a complete lattice
of a complete lattice 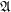 is chain-meet-closed iff for every filter base
is chain-meet-closed iff for every filter base 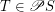 we have
we have 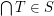 .
. Keywords: chain; complete lattice; filter bases; filters; linear order; total order
Co-separability of filter objects ★★
Author(s): Porton
 and
and  are filters on a set
are filters on a set 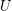 and
and 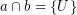 . Then
. Then 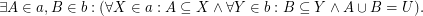
See here for some equivalent reformulations of this problem.
This problem (in fact, a little more general version of a problem equivalent to this problem) was solved by the problem author. See here for the solution.
Maybe this problem should be moved to "second-tier" because its solution is simple.
Keywords: filters
Pseudodifference of filter objects ★★
Author(s): Porton
Let 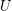 is a set. A filter
is a set. A filter 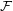 (on
(on 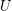 ) is a non-empty set of subsets of
) is a non-empty set of subsets of 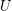 such that
such that 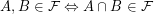 . Note that unlike some other authors I do not require
. Note that unlike some other authors I do not require 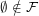 .
.
I will call the set of filter objects the set of filters ordered reverse to set theoretic inclusion of filters, with principal filters equated to the corresponding sets. See here for the formal definition of filter objects. I will denote 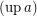 the filter corresponding to a filter object
the filter corresponding to a filter object  . I will denote the set of filter objects (on
. I will denote the set of filter objects (on 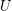 ) as
) as 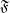 .
.
I will denote  the set of atomic lattice elements under a given lattice element
the set of atomic lattice elements under a given lattice element  . If
. If  is a filter object, then
is a filter object, then  is essentially the set of ultrafilters over
is essentially the set of ultrafilters over  .
.
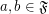 for each set
for each set 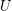 ? (If some are not equal, provide counter-examples.)
? (If some are not equal, provide counter-examples.)- \item
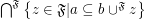 ;
;
\item 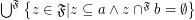 ;
;
\item 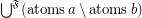 ;
;
\item 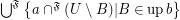 .
.
Keywords: filters; pseudodifference

 Drupal
Drupal CSI of Charles University
CSI of Charles University