 login/create account
login/create account
reloids
Restricting a reloid to lattice Gamma before converting it into a funcoid ★★
Author(s): Porton
Conjecture 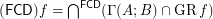 for every reloid
for every reloid 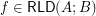 .
.
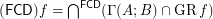 for every reloid
for every reloid 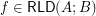 .
. Keywords: funcoid corresponding to reloid; funcoids; reloids
Inner reloid through the lattice Gamma ★★
Author(s): Porton
Conjecture 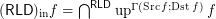 for every funcoid
for every funcoid  .
.
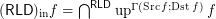 for every funcoid
for every funcoid  .
. Counter-example: 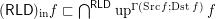 for the funcoid
for the funcoid 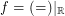 is proved in this online article.
is proved in this online article.
Keywords: filters; funcoids; inner reloid; reloids

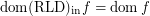 and
and 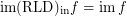 for every funcoid
for every funcoid  Drupal
Drupal CSI of Charles University
CSI of Charles University