 login/create account
login/create account
Domain and image of inner reloid (Solved)
Conjecture 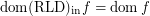 and
and 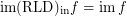 for every funcoid
for every funcoid  .
.
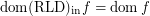 and
and 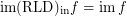 for every funcoid
for every funcoid  .
. See Algebraic General Topology for definitions of used concepts.
Proved positively in this online atticle
Bibliography
*Victor Porton. Algebraic General Topology
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University