 login/create account
login/create account
pseudodifference
Pseudodifference of filter objects ★★
Author(s): Porton
Let 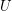 is a set. A filter
is a set. A filter 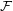 (on
(on 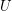 ) is a non-empty set of subsets of
) is a non-empty set of subsets of 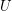 such that
such that 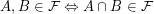 . Note that unlike some other authors I do not require
. Note that unlike some other authors I do not require 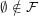 .
.
I will call the set of filter objects the set of filters ordered reverse to set theoretic inclusion of filters, with principal filters equated to the corresponding sets. See here for the formal definition of filter objects. I will denote 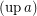 the filter corresponding to a filter object
the filter corresponding to a filter object  . I will denote the set of filter objects (on
. I will denote the set of filter objects (on 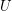 ) as
) as 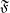 .
.
I will denote  the set of atomic lattice elements under a given lattice element
the set of atomic lattice elements under a given lattice element  . If
. If  is a filter object, then
is a filter object, then  is essentially the set of ultrafilters over
is essentially the set of ultrafilters over  .
.
Problem Which of the following expressions are pairwise equal for all 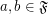 for each set
for each set 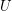 ? (If some are not equal, provide counter-examples.)
? (If some are not equal, provide counter-examples.)
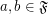 for each set
for each set 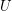 ? (If some are not equal, provide counter-examples.)
? (If some are not equal, provide counter-examples.)- \item
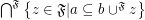 ;
;
\item 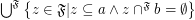 ;
;
\item 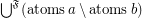 ;
;
\item 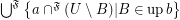 .
.
Keywords: filters; pseudodifference

 Drupal
Drupal CSI of Charles University
CSI of Charles University