 login/create account
login/create account
Graham's conjecture on tree reconstruction
 , we let
, we let 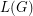 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 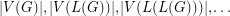 ?
? Graph reconstruction is a notoriously difficult subject. This conjecture is an unusual type of reconstruction problem where our class of graphs is very limited - just trees, but we are also given relatively little information - just a sequence of integers.
Bibliography
[GR] C. Godsil and G. Royle, Algebraic graph theory. Graduate Texts in Mathematics, 207. Springer-Verlag, New York, 2001 (page 18).
* indicates original appearance(s) of problem.
Graph theory
Does for any tree T there exist n that L^n(T) is a regular graph? Or perhaps for all graph?
No
Consider L^i(T) is a graph with "even triangle"(triangle with even degrees of vertices) subgraph. Edges of even triangle produce new even triangle in L^(i+1)(T). And if there is an odd degree vertex adjacent to parent triangle, there would be another one adjacent to child. So, irregular subgraph remains.
If G is a star graph of
If G is a star graph of order 5, then L(G) = K_5.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Reference
Could someone pleas give a proper reference? If I'm not mistaken, the problem is just *mentioned* in G&R, without references (anyway, I didn't find any).