 login/create account
login/create account
Graham, Ronald L.
Termination of the sixth Goodstein Sequence ★
Author(s): Graham
Question How many steps does it take the sixth Goodstein sequence to terminate?
Keywords: Goodstein Sequence
Monotone 4-term Arithmetic Progressions ★★
Author(s): Davis; Entringer; Graham; Simmons
Question Is it true that every permutation of positive integers must contain monotone 4-term arithmetic progressions?
Keywords: monotone arithmetic progression; permutation
Pebbling a cartesian product ★★★
Author(s): Graham
We let  denote the pebbling number of a graph
denote the pebbling number of a graph  .
.
Conjecture 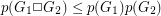 .
.
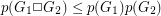 .
. Divisibility of central binomial coefficients ★★
Author(s): Graham
Problem (1) Prove that there exist infinitely many positive integers  such that
such that 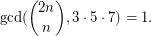
 such that
such that 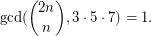
Problem (2) Prove that there exists only a finite number of positive integers  such that
such that 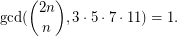
 such that
such that 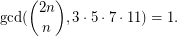
Keywords:
The large sets conjecture ★★★
Author(s): Brown; Graham; Landman
Conjecture If  is 2-large, then
is 2-large, then  is large.
is large.
 is 2-large, then
is 2-large, then  is large.
is large. Keywords: 2-large sets; large sets
Graham's conjecture on tree reconstruction ★★
Author(s): Graham
Problem for every graph  , we let
, we let 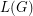 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 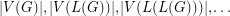 ?
?
 , we let
, we let 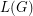 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 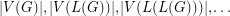 ?
? Keywords: reconstruction; tree

 Drupal
Drupal CSI of Charles University
CSI of Charles University