 login/create account
login/create account
reconstruction
Switching reconstruction conjecture ★★
Author(s): Stanley
Conjecture Every simple graph on five or more vertices is switching-reconstructible.
Keywords: reconstruction
Edge Reconstruction Conjecture ★★★
Author(s): Harary
Conjecture
Every simple graph with at least 4 edges is reconstructible from it's edge deleted subgraphs
Keywords: reconstruction
Reconstruction conjecture ★★★★
The deck of a graph  is the multiset consisting of all unlabelled subgraphs obtained from
is the multiset consisting of all unlabelled subgraphs obtained from  by deleting a vertex in all possible ways (counted according to multiplicity).
by deleting a vertex in all possible ways (counted according to multiplicity).
Conjecture If two graphs on 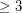 vertices have the same deck, then they are isomorphic.
vertices have the same deck, then they are isomorphic.
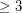 vertices have the same deck, then they are isomorphic.
vertices have the same deck, then they are isomorphic. Keywords: reconstruction
Graham's conjecture on tree reconstruction ★★
Author(s): Graham
Problem for every graph  , we let
, we let 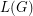 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 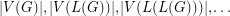 ?
?
 , we let
, we let 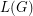 denote the line graph of
denote the line graph of  . Given that
. Given that  is a tree, can we determine it from the integer sequence
is a tree, can we determine it from the integer sequence 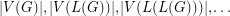 ?
? Keywords: reconstruction; tree

 Drupal
Drupal CSI of Charles University
CSI of Charles University