 login/create account
login/create account
To switch a vertex of a simple graph is to exchange its sets of neighbours and non-neighbours. The graph so obtained is called a switching of the graph. The collection of switchings of a graph G is called the switching deck of  . A graph is switching-reconstructible if every graph with the same deck as
. A graph is switching-reconstructible if every graph with the same deck as  is isomorphic to
is isomorphic to  .
.
There are four pairs of non-isomorphic graphs of order  with the same switching deck. One of them consists of the empty graph and the
with the same switching deck. One of them consists of the empty graph and the  -cycle.
-cycle.
Stanley [S] proved that a graph on  vertices is switching-reconstructible if
vertices is switching-reconstructible if 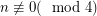 .
.
An analogous problem was posed for digraphs. Instead of complementing the edges at a vertex, one reverses each of its incident arc.
Bibliography
*[S] R. P. Stanley Reconstruction from vertex-switching. J. Combin. Theory Ser. B, 38 (1985), 132--138.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University