To switch a vertex of a digraph is to reverse all the arcs incident to it. The digraph so obtained is called a switching of the digraph. The collection of switchings of a digraph is called the switching deck of . A digraph is switching-reconstructible if every digraph with the same deck as is isomorphic to .

The problem is a directed analogue of switching reconstruction of graphs in which one complements the edges at a vertex, instead of reversing each of its incident arcs.

Bondy and Mercier proved an analogue to Stanley's result for switching reconstruction of graphs. They proved that a digraph on vertices is switching-reconstructible if 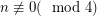. They also proved many other common results for both switching reconstructions.

One significant difference between the directed and undirected problems is that there exist switching-nonreconstructible directed graphs on eight vertices, while Stanley's conjecture that every simple graph on five or more vertices is switching-reconstructible.