 login/create account
login/create account
To switch a vertex of a digraph is to reverse all the arcs incident to it. The digraph so obtained is called a switching of the digraph. The collection of switchings of a digraph  is called the switching deck of
is called the switching deck of  . A digraph is switching-reconstructible if every digraph with the same deck as
. A digraph is switching-reconstructible if every digraph with the same deck as  is isomorphic to
is isomorphic to  .
.
The problem is a directed analogue of switching reconstruction of graphs in which one complements the edges at a vertex, instead of reversing each of its incident arcs.
Bondy and Mercier proved an analogue to Stanley's result for switching reconstruction of graphs. They proved that a digraph on  vertices is switching-reconstructible if
vertices is switching-reconstructible if 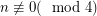 . They also proved many other common results for both switching reconstructions.
. They also proved many other common results for both switching reconstructions.
One significant difference between the directed and undirected problems is that there exist switching-nonreconstructible directed graphs on eight vertices, while Stanley's conjecture that every simple graph on five or more vertices is switching-reconstructible.
Bibliography
*[BM] J. A. Bondy and F. Mercier. Switching reconstruction of digraphs. J. Graph Theory 67(2011), no. 4, 332-348.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University