 login/create account
login/create account
Ulam, Stanislaw M.
Are there an infinite number of lucky primes? ★
Author(s): Lazarus: Gardiner: Metropolis; Ulam
Conjecture If every second positive integer except 2 is remaining, then every third remaining integer except 3, then every fourth remaining integer etc. , an infinite number of the remaining integers are prime.
Dense rational distance sets in the plane ★★★
Author(s): Ulam
Problem Does there exist a dense set 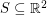 so that all pairwise distances between points in
so that all pairwise distances between points in 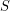 are rational?
are rational?
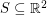 so that all pairwise distances between points in
so that all pairwise distances between points in 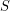 are rational?
are rational? Keywords: integral distance; rational distance
Reconstruction conjecture ★★★★
The deck of a graph  is the multiset consisting of all unlabelled subgraphs obtained from
is the multiset consisting of all unlabelled subgraphs obtained from  by deleting a vertex in all possible ways (counted according to multiplicity).
by deleting a vertex in all possible ways (counted according to multiplicity).
Conjecture If two graphs on 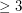 vertices have the same deck, then they are isomorphic.
vertices have the same deck, then they are isomorphic.
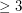 vertices have the same deck, then they are isomorphic.
vertices have the same deck, then they are isomorphic. Keywords: reconstruction

 Drupal
Drupal CSI of Charles University
CSI of Charles University