 login/create account
login/create account
Dense rational distance sets in the plane
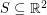 so that all pairwise distances between points in
so that all pairwise distances between points in  are rational?
are rational? This famous problem was asked by Ulam, who guessed the answer would be negative.
A cute theorem of Erdos shows that if 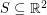 is non-collinear and all pairwise distances between points in
is non-collinear and all pairwise distances between points in  are integral, then
are integral, then  is finite. For the proof, first note that if
is finite. For the proof, first note that if 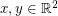 have distance
have distance 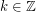 , then every point which has integer distance to both
, then every point which has integer distance to both  and
and 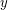 must lie on one of the
must lie on one of the 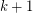 hyperbolas consisting of those
hyperbolas consisting of those 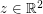 with
with 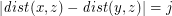 for some
for some 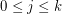 . So, if all pairwise distances between points in
. So, if all pairwise distances between points in  are integral, and
are integral, and 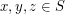 are non-collinear, then every other point in
are non-collinear, then every other point in  must lie on an intersection between one of finitely many hyperbola with foci
must lie on an intersection between one of finitely many hyperbola with foci 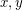 and one of finitely many with foci
and one of finitely many with foci 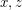 . This set is necessarily finite, thus completing the proof.
. This set is necessarily finite, thus completing the proof.
Of course, the above argument gives no upper bound on the size of a non-collinear set of points in 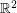 with pairwise integral distances. Indeed, if Ulam's conjecture is true, then there exist such sets of arbitrary size. Surprisingly, it is very difficult to construct such sets
with pairwise integral distances. Indeed, if Ulam's conjecture is true, then there exist such sets of arbitrary size. Surprisingly, it is very difficult to construct such sets  of even rather small size. Recently Kreisel and Kurz [KK] found such a set of size 7, but it is unknown if there exists one of size 8.
of even rather small size. Recently Kreisel and Kurz [KK] found such a set of size 7, but it is unknown if there exists one of size 8.
It is trivial to find infinitely many points on a line with all pairwise distances rational. Less trivially, there exist infinite subsets of a circle with all pairwise distances rational. Very recently, Solymosi and De Zeeuw [SZ] proved that these are the only two irreducible algebraic curves with this property. This suggests that, if the answer to Ulam's problem is affirmative, such a set  must be extremely special.
must be extremely special.
Bibliography
[KK] T. Kreisel and S. Kurz, There are integral heptagons, no three points on a line, no four on a circle, Discrete & Computational Geometry, Online first: DOI 10.1007/s00454-007-9038-6
[SZ] J. Solymosi and F. de Zeeuw, On a question of Erdos and Ulam.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University