 login/create account
login/create account
Nearly spanning regular subgraphs
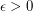 and every positive integer
and every positive integer  , there exists
, there exists 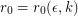 so that every simple
so that every simple  -regular graph
-regular graph  with
with 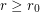 has a
has a  -regular subgraph
-regular subgraph  with
with 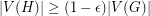 .
. Petersen's theorem asserts that every regular graph of even degree contains a 2-factor (i.e. a spanning 2-regular subgraph). Iterating this easy result we find that for any pair of positive even integers 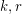 , every
, every  -regular graph has a spanning
-regular graph has a spanning  -regular subgraph. The cases when either
-regular subgraph. The cases when either  or
or  is odd are considerably more complicated. There are some nice general results (see [AFK]) which show that every regular graph of sufficiently high degree contains a
is odd are considerably more complicated. There are some nice general results (see [AFK]) which show that every regular graph of sufficiently high degree contains a  -regular subgraph. However these theorems give no bound on the size of this subgraph.
-regular subgraph. However these theorems give no bound on the size of this subgraph.
For 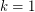 this conjecture is an easy consequence of Vizing's Theorem. Indeed, this theorem implies that every
this conjecture is an easy consequence of Vizing's Theorem. Indeed, this theorem implies that every  -regular graph
-regular graph  has a 1-regular subgraph
has a 1-regular subgraph  with
with 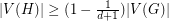 (just choose a largest color class from a
(just choose a largest color class from a 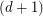 -edge coloring). Alon [A] proved the conjecture for
-edge coloring). Alon [A] proved the conjecture for 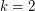 with the help of two famous results on permanents: the Minc Conjecture (proved by Bregman), and the van der Waerden conjecture (proved by Falikman and Egorichev). It is open for all
with the help of two famous results on permanents: the Minc Conjecture (proved by Bregman), and the van der Waerden conjecture (proved by Falikman and Egorichev). It is open for all 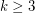 .
.
Bibliography
*[A] N. Alon, Problems and results in extremal combinatorics, J, Discrete Math. 273 (2003), 31-53.
[AFK] N. Alon, S. Friedland and G. Kalai, Regular subgraphs of almost regular graphs, J. Combinatorial Theory, Ser. B 37(1984), 79-91.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University